Quantum Computing has the potential to speed up many financial use cases. To make this happen, we need new algorithmic developments that leverage new hardware features. Our work is a great example of this progress, bringing the industry closer to solving financial use cases with Quantum Computing.
Quantum computing for portfolio optimization
Quantum computing is poised to revolutionize computational finance. However, the capabilities of current quantum hardware significantly constrain the scale of experimental demonstrations. This makes it challenging to perform demonstrations on hardware of quantum algorithms for practically relevant use cases.
Portfolio optimization is an important use case in finance that lends itself to be tackled by quantum computing. The Harrow-Hassidim-Lloyd (HHL) algorithm solves linear systems of equations, and it can be used to solve portfolio optimization by casting this problem into a linear system. HHL solves a quantum version of the linear systems problem, whose solution can allow to observe useful properties about the optimal portfolio. However, most of the components of HHL are far out of the reach of noisy intermediate-scale quantum devices, which has led to the proposal of hybrid classical-quantum variants that leverage the power of both classical and quantum computation.
We introduce Hybrid HHL++ that bridges the gap between proposed near-term implementations of HHL and the kinds of quantum circuits that can be executed on today’s hardware. To demonstrate the effectiveness of our procedure, we successfully applied Hybrid HHL++ to small-scale portfolio-optimization problems on the Quantinuum System Model H-series trapped-ion quantum computers. This Hybrid HHL++ research paper has just been published in Nature Scientific Reports.
Our novel contributions
Common challenges for implementing quantum algorithms on current hardware are the limited number of qubits, typically ranging from tens to hundreds on near-term devices, and the fact that deep circuits are prone to hardware noise. To address them we make two novel contributions: (1) propose a novel algorithm that maximizes the utility of the number of ancillary qubits, by determining a scaling factor for the linear system matrix, and (2) introduce a heuristic for compressing the HHL circuit.
We demonstrate the efficacy of our work by running Hybrid HHL++ on the Quantinuum System Model H-series trapped-ion quantum computers to solve different problem instances of small-scale portfolio optimization problems, leading to the largest experimental demonstrations of HHL for an application to date.
The efficiency of the proposed algorithm is evaluated by different figures of merit, including the inner product, as shown in Figure 1 and Table 1. The quality of the solution to the portfolio-optimization problems is very high, and close to the one obtained in noiseless simulation, illustrating thar our proposed algorithm Hybrid HHL++ is more robust to hardware noise. This work represents a milestone towards the evaluation of quantum algorithms to tackle relevant use cases in quantum hardware available today.
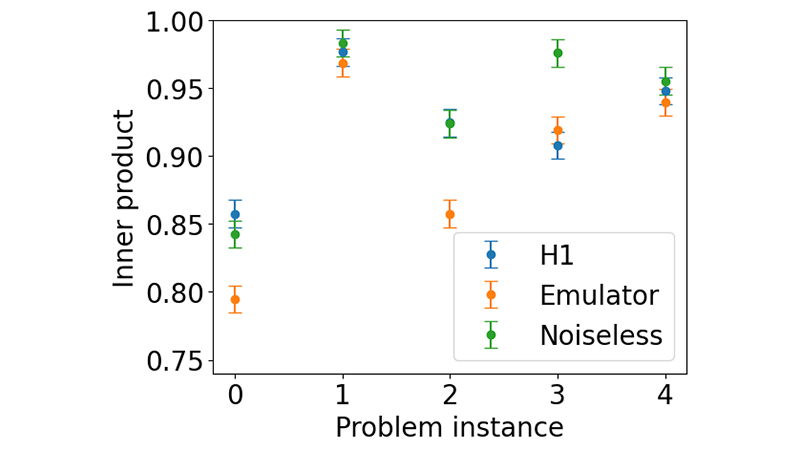
The infographic illustrates the inner product that measures the quality of the solution obtained with Hybrid HHL++ for each of the portfolio-optimization problem instances considered.
Short description:
Plot of the inner product between the output quantum state of Hybrid HHL++ and the analytical solution for each of the portfolio-optimization problem instances with two assets.
Long description:
The inner product quantifies the quality of the solution obtained, being the closer to 1, the better the solution. Displayed is the inner product corresponding to the execution of the circuits on hardware, its emulator with approximated noise and in noiseless simulation.
Figure 1: Inner product between the output quantum state of Hybrid HHL++ and the analytical solution for each of the portfolio-optimization problem instances with two assets. The inner product quantifies the quality of the solution obtained, being the closer to 1, the better the solution. It is displayed the inner product corresponding to the execution of the circuits on hardware, its emulator with approximated noise and in noiseless simulation.
The infographic illustrates the main results in terms of the quality of the solution obtained by Hybrid HHL++ on quantum hardware, its emulator and noiseless simulation.
Short description:
Summary of the results obtained in terms of the inner product. Shown is the number of qubits and depth of the circuits of the implementation of Hybrid HHL++.
Long description:
It is observed that the inner product (i.e., quality of the solution) obtained on hardware (H1 device) overlaps with the quality obtained on noiseless simulation, illustrating that the proposed algorithm Hybrid HHL++ is more resistant to hardware noise.
Table 1: Summary of the results obtained, where we show the number of qubits utilized and the circuit depth. It is observed that the inner product (i.e., quality of the solution) obtained on hardware (H1 device) overlaps with the quality obtained on noiseless simulation, illustrating that the proposed algorithm Hybrid HHL++ is more resistant to hardware noise.
To learn more about Global Technology Applied Research at JPMorganChase, please visit https://www.jpmorgan.com/technology/applied-research.